Crafting Worlds: Procedural Level Generation in Slide
I've been spending a lot of time lately building out the level generation system for my Android game, Slide. It's been an interesting dive into the world of procedural content generation (PCG), and I wanted to share some of the technical details. It's surprisingly complex to create levels that feel solvable and fun, even with a simple 2D game like this.
The Core Idea: Constraints and Validation
The basic premise of Slide is to move a character around a grid, activating switches and pushing blocks before you can reach your goal. The challenge lies in creat.ing levels that aren't trivially easy, but also aren't impossible. My approach breaks down into two main stages: generation and validation. First we generate a level layout, and then we check to make sure that the game is actually solvable and meets our design goals.

This is a common pattern in PCG--generate a candidate, then ruthlessly filter it. From a computer science perspective, this can be framed as a search problem. We're searching for a level configuration that satisfies a set of constraints. The generation phase is akin to proposing a solution, and the validation phase is evaluating its feasibility.
Level Generation
We start with a grid and populate it with tiles. The tiles themselves are fairly simple: empty space, walls, and directional ramps. The generation process leverages probabilistic modeling. We don't simply place tiles randomly; instead, we assign probabilities to each tile type based on the desired difficulty. For example, on "easy" difficulty, empty space is much more likely than walls. This is achieved through a weighted random selection process.
This approach allows us to tune parameters--the tile weights--to control the overall "openness" and complexity of the levels. It's similar to adjusting hyperparameters in a machine learning model. We experiment with different weightings to achieve a desired distribution of level characteristics.
Validation
Generating is a start--we also need to verify that it's actually solvable. We now perform a series of quick checks to ensure the level data is well-formed and meets basic criteria.
However, these checks aren't sufficient. We need to prove that a solution exists. This is achieved using a graph search algorithm, specifically Breadth-First Search (BFS). We can represent the level as a graph, where each tile is a node and valid moves between tiles are edges. BFS systematically explores the graph, starting from the start position, until it reaches the finish.
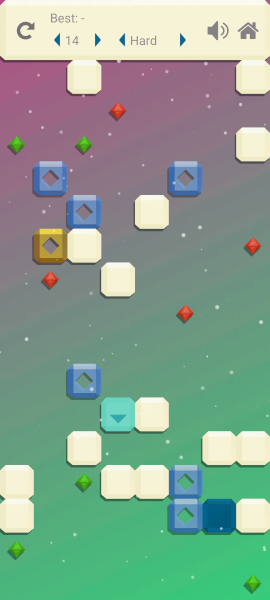
Once you start adding extra elements to the puzzle, for instance an on/off switch or a moveable block, the complexity of the state space increases exponentially. For instance, adding a block that you can push around the grid adds new elements to the search space. The more blocks you add, the more this starts to explode in complexity. Modern processors are fast, but with a big enough level this method of solving the puzzle would eventually become computationally infeasible.
The initial parameters (tile weights, grid size, maximum search depth) are chosen through experimentation. We generate a large number of levels, validate them, and analyze the results. This helps us fine-tune the parameters to achieve the desired difficulty curve and level quality.
Future Directions
My current approach has created some genuinely challenging and interesting levels, but when I compare them to hand-crafted levels I made 9 years ago, the difference is obvious. Because of the randomness of the level-generation process the generated levels contain many tiles that are unused, inaccessible, or just irrelevant to the puzzle. In other words, the amount of content in the PCG levels is lower than in the hand-crafted levels. I'm sure there is some way to refine the algorithm to address this, but for now this is an open problem.
I'm exploring more advanced techniques, such as:
-Constraint Satisfaction Problems (CSPs): Formulating the level generation as a CSP allows us to specify more complex constraints and use specialized solvers. This is a more declarative approach to level design, where we define what we want, rather than how to achieve it.
-Machine Learning: You might think that it would be easy enough to just feed a bunch of training examples to an large language model, but it turns out in practice this is not yet feasible. Maybe a fun AGI bench mark would be a test to see if a model can consistently produce levels based on a series of training examples. But alas, we are not there yet, and it is much more reliable to stick to good ol' fashioned AI.
I hope this gives you a glimpse into what the heck I've been doing with my free time. Let me know if you have any questions!